Привет, мой читатель.
На днях встретил простую на вид задачу. Как оказалось, не легко решить такую задачу за пять, и даже за 50 минут. Здесь пришлось подумать и поэкспериментировать.
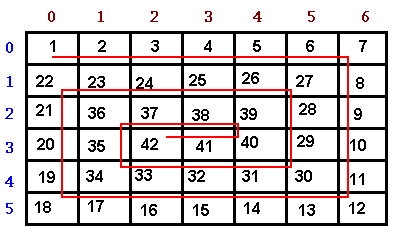
Дана матрица, или, на нашем языке, двумерный массив. Его размеры не могут превышать 10х10. Они задаются пользователем и это может быть не только квадрат, но и прямоугольник. Обозначим длины сторон через N и M. Нам необходимо заполнить эту матрицу числами от 1 и по возрастающей до M*N. Прежде, чем привести код целиком, мне хотелось бы изложить ход мыслей, чтобы стало понятно как все работает. Если же тебе просто нужно решение, то ты можешь пролистать ниже, скопировать его и закрыть страницу как больше не нужную.
Стандартно, нам нужен сам массив и переменные для хранения длин сторон прямоугольного (двумерного) массива.
int a[10][10] = {0};
int N, M;
Также мы будем действовать по слогике, что при заполнении мы очерчиваем прямоугольники, каждый их которых на единицу меньше с каждой стороны. Если смотреть на эти прямоугольники в декартовой системе координат, то начало каждой из сторон сдвигается на 1 вправо или вниз, а конец влево или вверх. Договоримся, что оси направлены вправо и вниз от точки [0,0].
Таким образом нам нужно знать точки начала и конца очерчиваемого прямоугольника. Это и будут точки излома (поворота). Но я еще и решил пойти следующим путем. Точки конца сторон будут равняться длине стороны первого прямоугольника минус длине текущего прямоугольника.
Обозначим их следующим образом:
int Ibeg = 0, Ifin = 0, Jbeg = 0, Jfin = 0;
Ну, и, нам нужна переменная, значением которой мы будем заполнять массив, пока она не достигнет значения M*N
int k = 1;
В цикле начинаем заполнять массив. Сначала точке a[i][j] присваиваем значение k. Это удобно тем, что если длина сторон равна 0, то мы не войдем в массив. Иначе в точку a[i][j] положим значение k, в конце же цикла инкреминируем его.
a[i][j] = k; /** * Код между началом и концом цикла */ ++k;
Далее вычисляем следующий шаг
- Если у нас верхняя сторона прямоугольника и мы не достигла правой стороны, то двигаемся вправо: ++j
- Если мы на правой стороне прямоугольника и не достигли нижней стороны, то двигаемся вниз: ++i
- Если мы на нижней стороне прямоугольника и не достигли левой стороны, то двигаемся влево: --j
- Иначе двигаемся вверх: --i
if (i == Ibeg && j < M - Jfin - 1)
++j;
else if (j == M - Jfin - 1 && i < N - Ifin - 1)
++i;
else if (i == N - Ifin - 1 && j > Jbeg)
--j;
else
--i;
В конце же каждого прохода проверяем, завершился ли прямоугольник и стои ли начинать прочерчивать новый - меньший:
- Если мы находимся на второй строке
- Если мы находимся на первом столбце
- И, в случае, если чертим не прямоугльник, а вертикальную линию, если первая строка не равна последней. (этот пункт самый сложный во всем алгоритме. Его я достиг путем экспериментов)
Тогда увеличиваем отступы от краев первого прямоугольника:
if ((i == Ibeg + 1) && (j == Jbeg) && (Jbeg != M - Jfin - 1)){
++Ibeg;
++Ifin;
++Jbeg;
++Jfin;
}
Собственно это весь алгоритм. А ниже код всей программы:
#include
int main()
{
int a[10][10] = {0};
int N, M;
scanf("%d%d", &N, &M);
int Ibeg = 0, Ifin = 0, Jbeg = 0, Jfin = 0;
int k = 1;
int i = 0;
int j = 0;
while (k <= N * M){
a[i][j] = k;
if (i == Ibeg && j < M - Jfin - 1)
++j;
else if (j == M - Jfin - 1 && i < N - Ifin - 1)
++i;
else if (i == N - Ifin - 1 && j > Jbeg)
--j;
else
--i;
if ((i == Ibeg + 1) && (j == Jbeg) && (Jbeg != M - Jfin - 1)){
++Ibeg;
++Ifin;
++Jbeg;
++Jfin;
}
++k;
}
for (int i = 0; i < 10; ++i){
for (int j = 0; j < 10; ++j)
printf("%3d", a[i][j]);
printf("\n");
}
return 0;
}
Я видел более изящные решения данной задачи, наполненные математикой и побитовыми операциями. Но для понимания того, как последовательно наполняется пассив по спирали, достаточно данного алгоритма. Буду рад, если вы оставите в комментариях свои решения и поделитесь мыслями.